Computational Fluid Dynamics as good as it gets.

A conservative integration of the pseudo-incompressible equations with implicit turbulence parameterization

F. Rieper, S. Hickel, U. Achatz (2013)
Monthly Weather Review 141: 861-886. doi: 10.1175/MWR-D-12-00026.1

Durran’s pseudo-incompressible equations are integrated in a mass and momentum conserving way with a new implicit turbulence model. This system is soundproof, which has two major advantages over fully compressible systems: the Courant–Friedrichs–Lewy (CFL) condition for stable time advancement is no longer dictated by the speed of sound and all waves in the model are clearly gravity waves (GW).

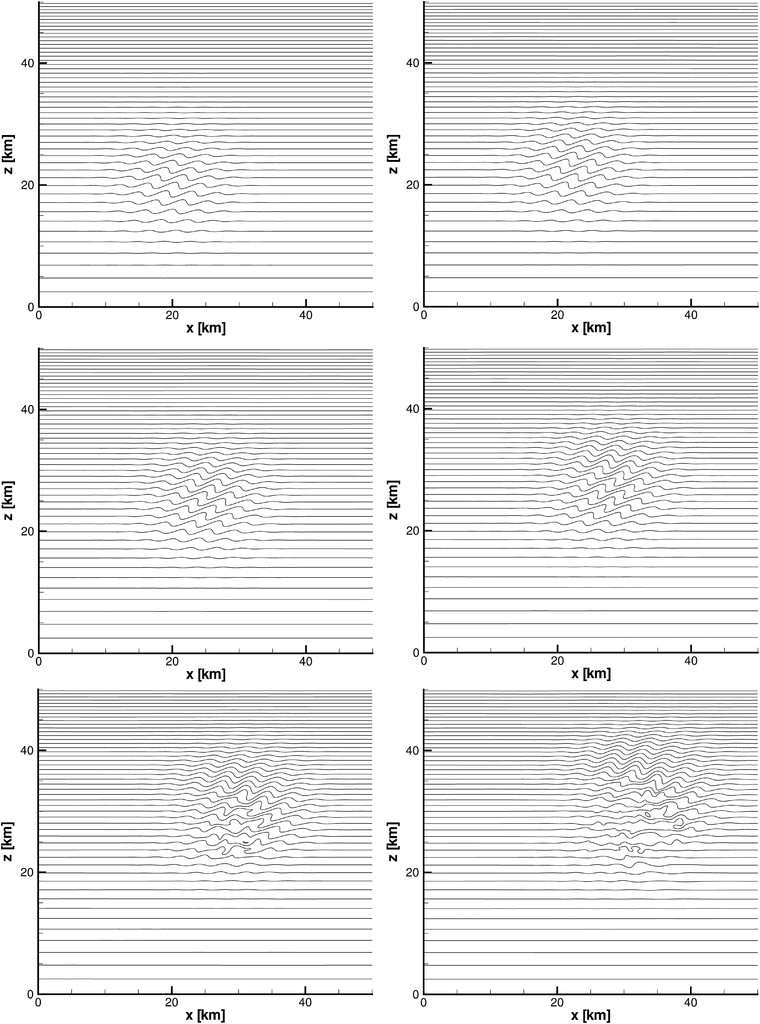
Thus, the pseudo-incompressible equations are an ideal laboratory model for studying GW generation, propagation, and breaking. Gravity wave breaking creates turbulence that needs to be parameterized. For the first time the adaptive local deconvolution method (ALDM) for implicit large-eddy simulation (ILES) is applied to non-Boussinesq stratified flows. ALDM provides a turbulence model that is fully merged with the discretization of the flux function. In the context of non-Boussinesq stratified flows this poses some new numerical challenges—the solution of which is presented in this text. In numerical test cases the authors show the agreement of the results with the literature (Robert’s hot–cold bubble test case), they present the sensitivity to the model’s resolution and discretization, and they demonstrate qualitatively the behavior of the implicit turbulence model for a 2D breaking gravity wave packet.

 

 

Isolines of density perturbation for Robert’s test case (left) without initial wind and (right) with a uniform mean wind u0 = 1.67 m/s. (top center) Initial setting (second row) after 10/3 minutes, (third row) after 20/3 minutes, and (bottom row) after 10 min calculated with ALDM on a 200 × 200 grid. Spacing of contour lines are from ρ′ = −2.2 to ρ′ = 0.5 g m−3 in steps of Δρ′ = 0.3 g m−3.

 

Isolines of the total potential temperature for a breaking 2D gravity wave packet. (left)–(right) and (top)–(bottom) After 0, 10, 20, 30, 40, and 50 min.

 

Publications