Computational Fluid Dynamics as good as it gets.

Cut-element based immersed boundary method for moving geometries in compressible liquid flows with cavitation

F. Örley, V. Pasquariello, S. Hickel, N.A. Adams (2015) 
Journal of Computational Physics 283: 1-22.  doi: 10.1016/j.jcp.2014.11.028

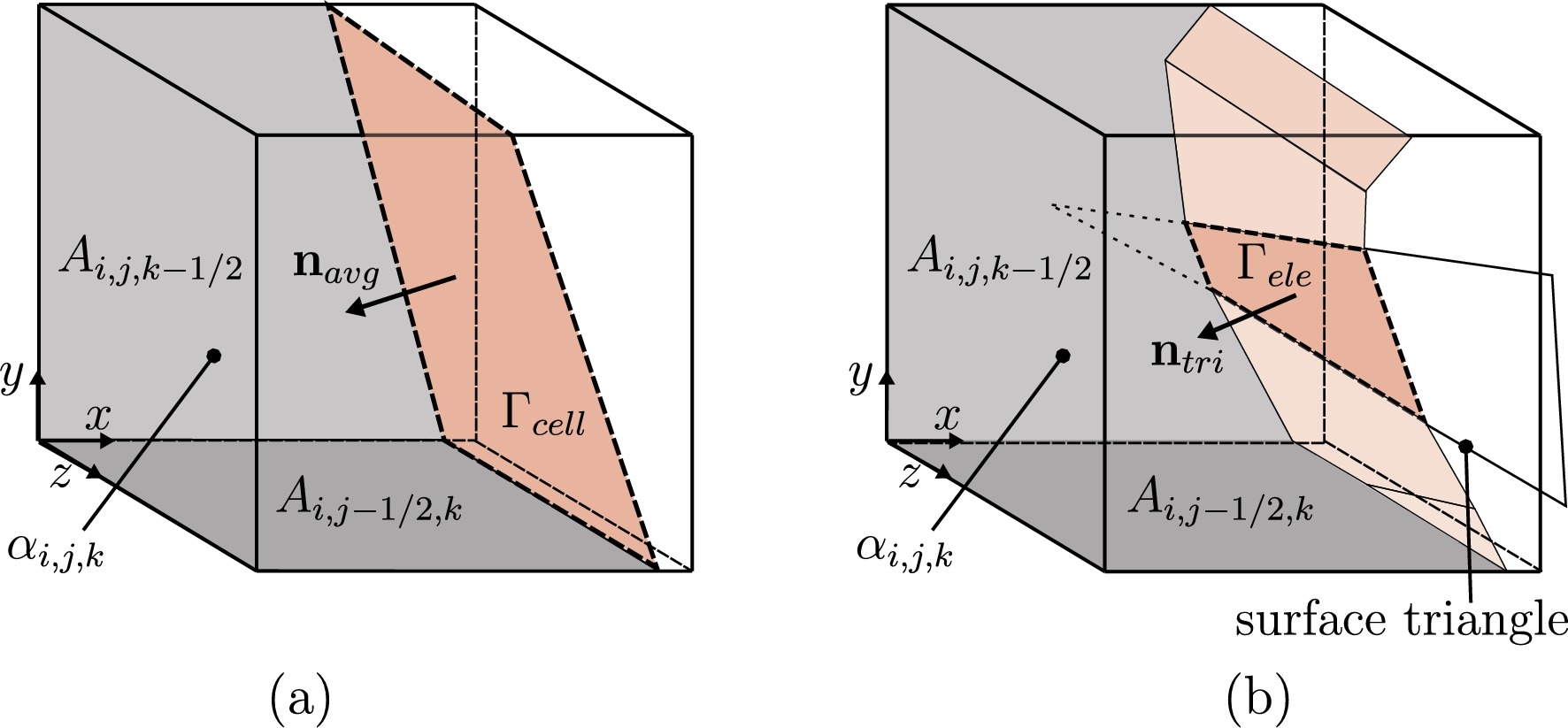
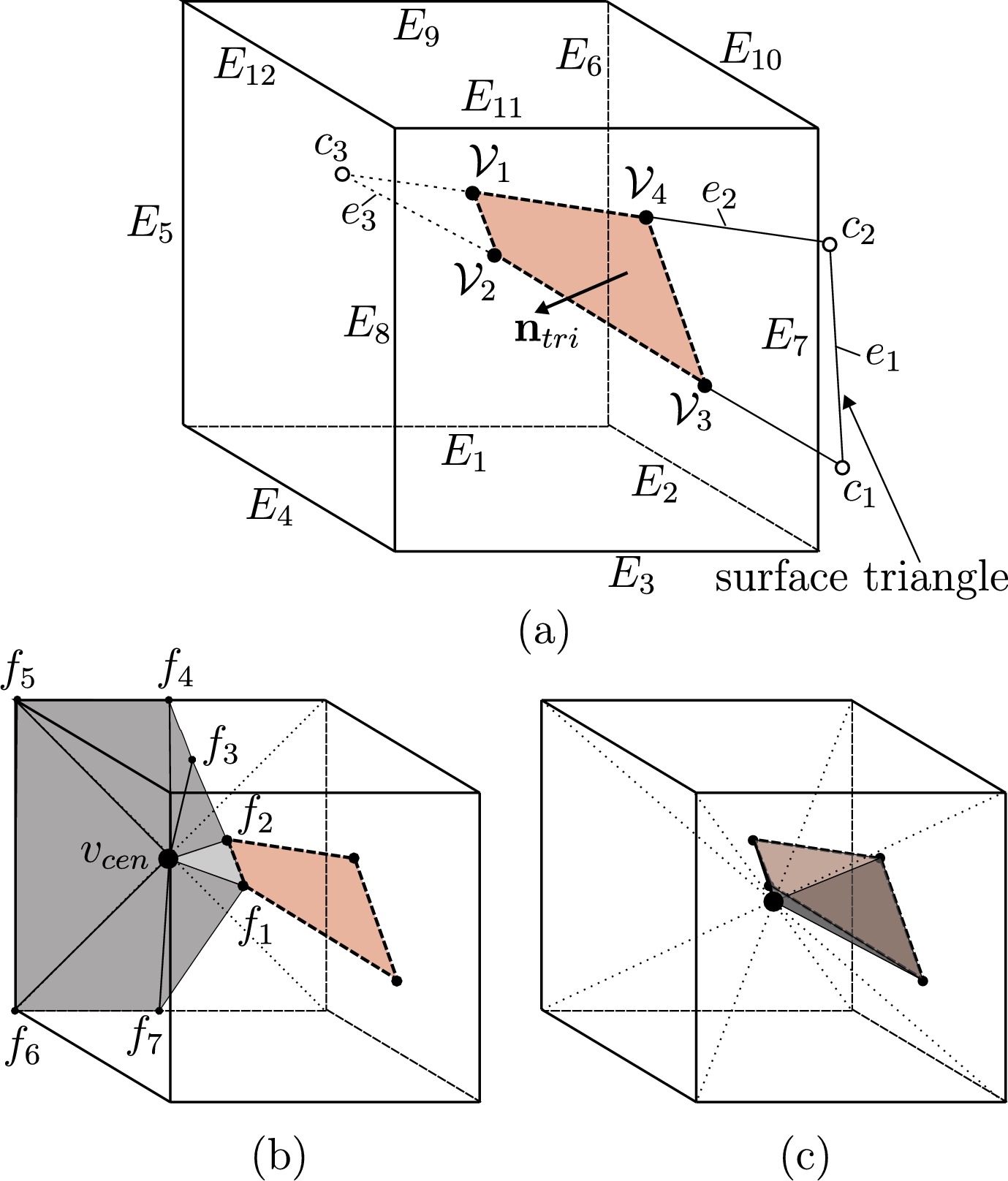
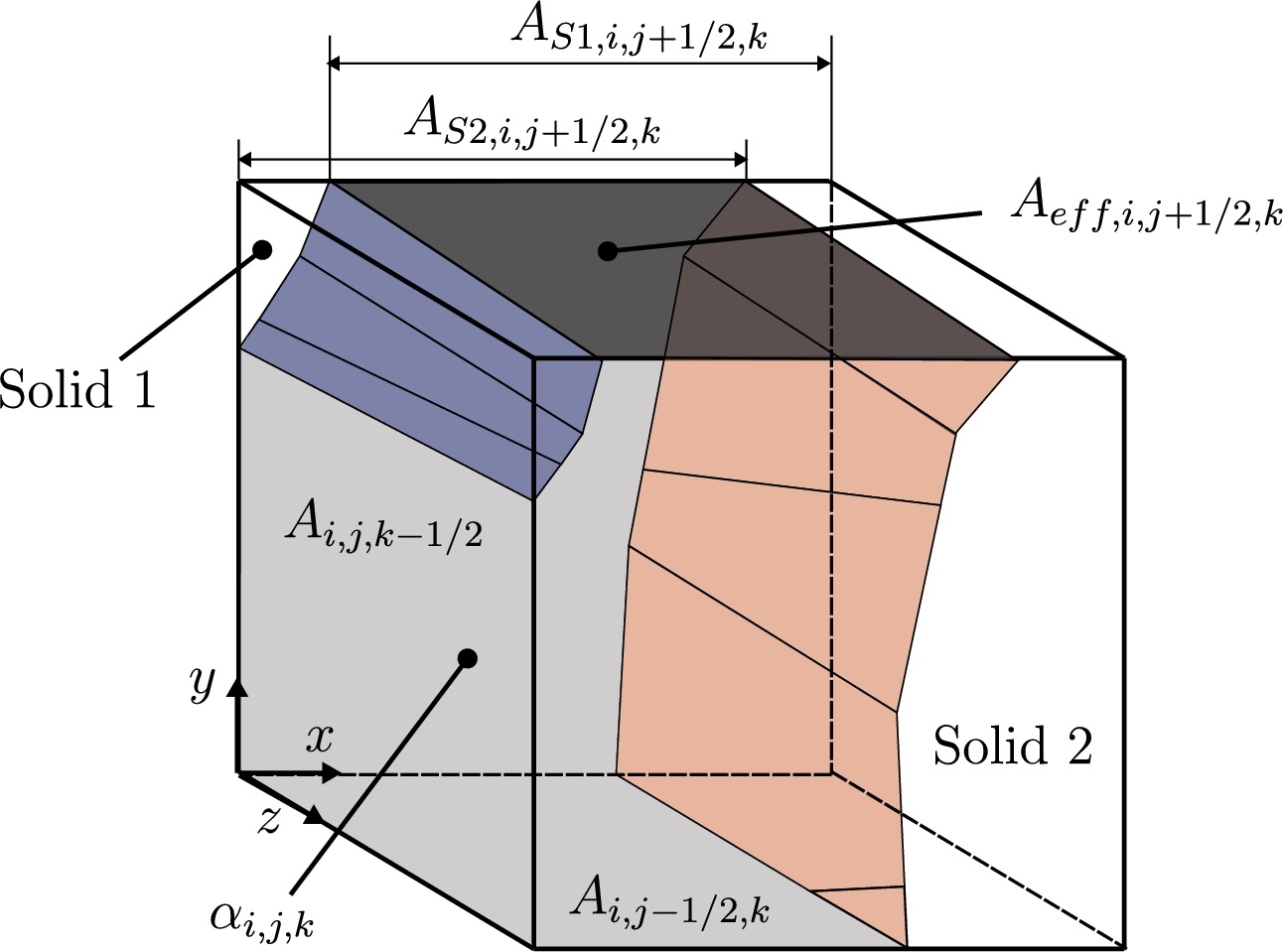
The conservative immersed interface method for representing complex immersed solid boundaries or phase interfaces on Cartesian grids is improved and extended to allow for the simulation of weakly compressible fluid flows through moving geometries. We demonstrate that an approximation of moving interfaces by a level-set field results in unphysical oscillations in the vicinity of sharp corners when dealing with weakly compressible fluids such as water. By introducing an exact reconstruction of the cut-cell properties directly based on a surface triangulation of the immersed boundary, we are able to recover the correct flow evolution free of numerical artifacts.

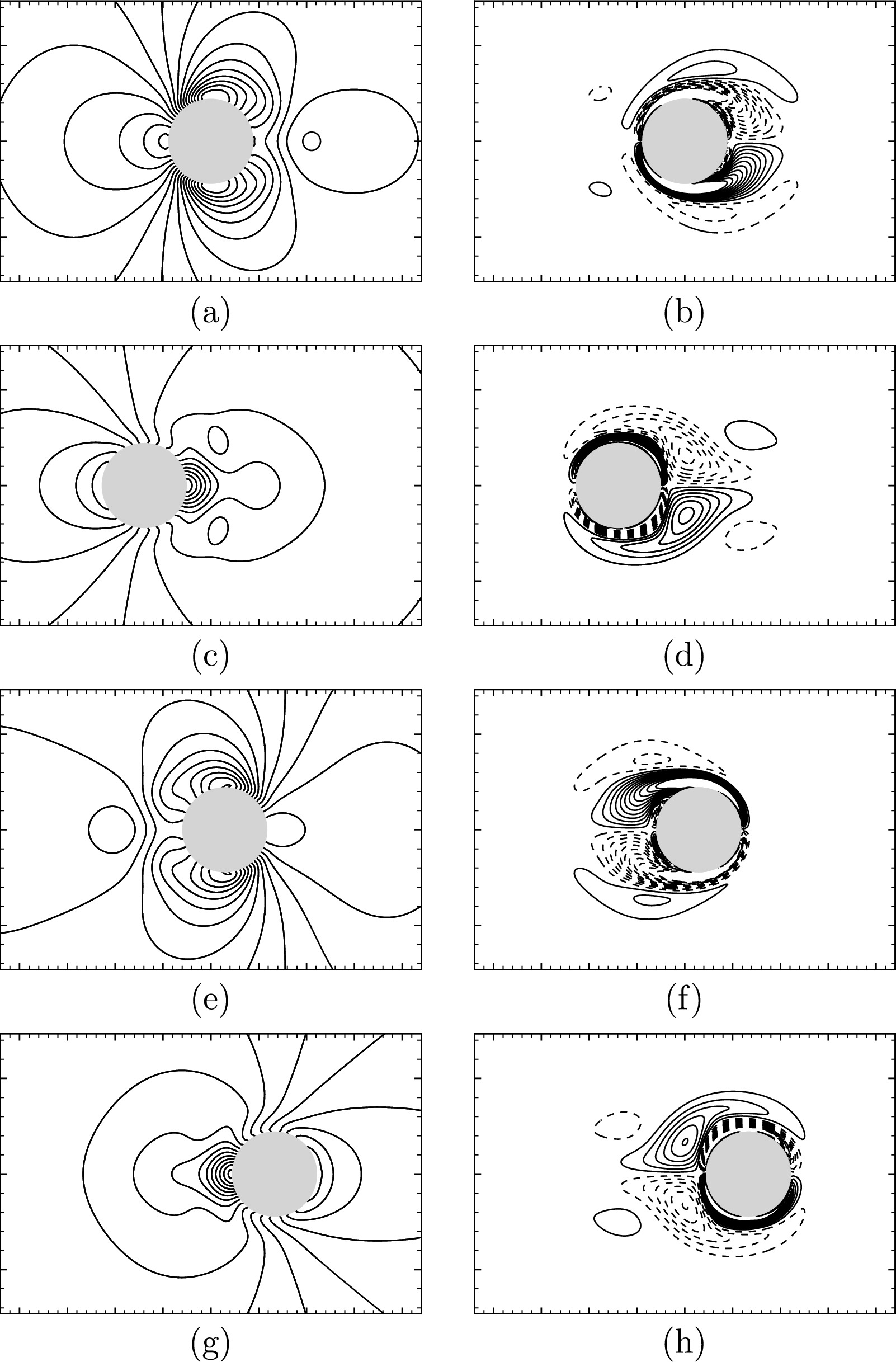
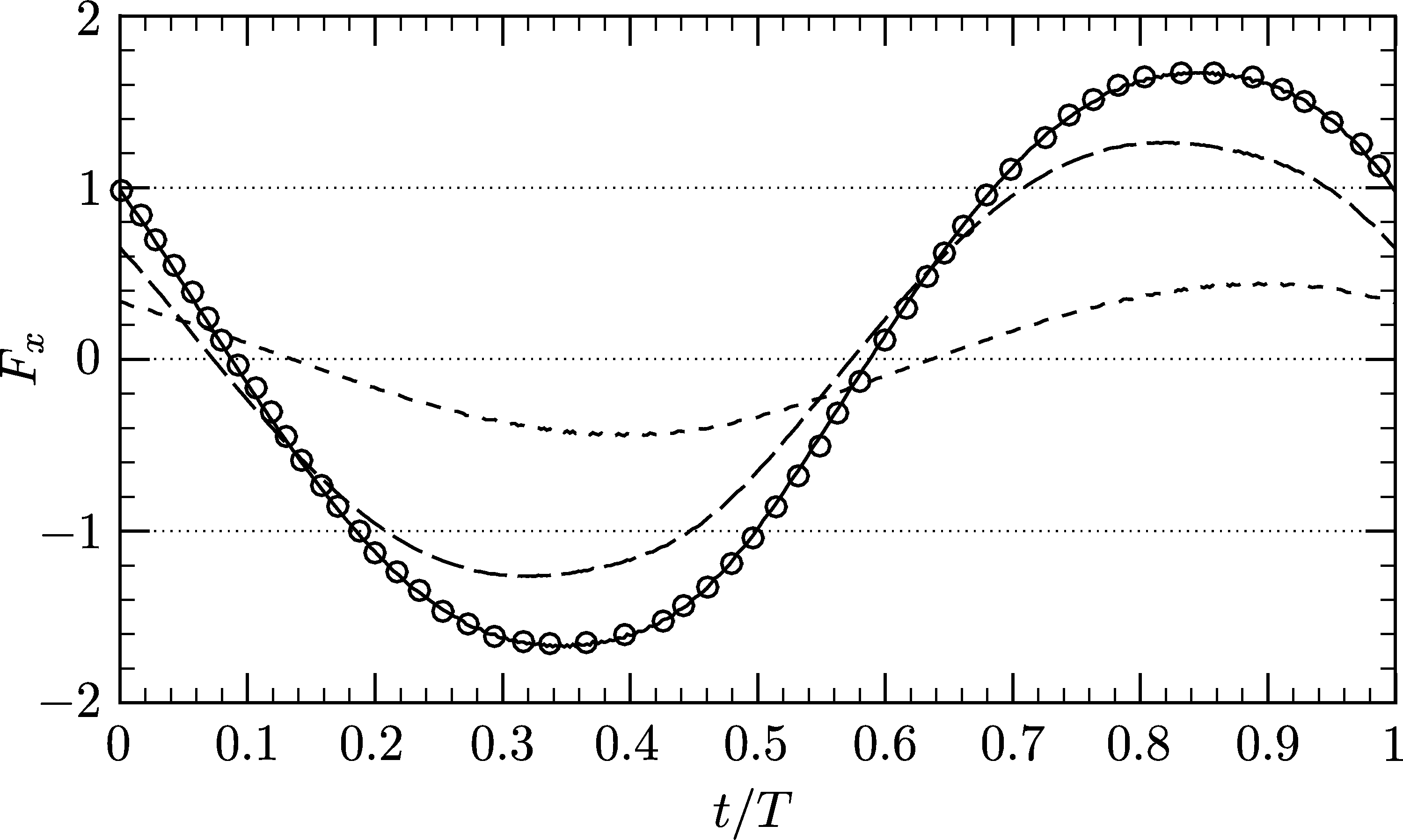
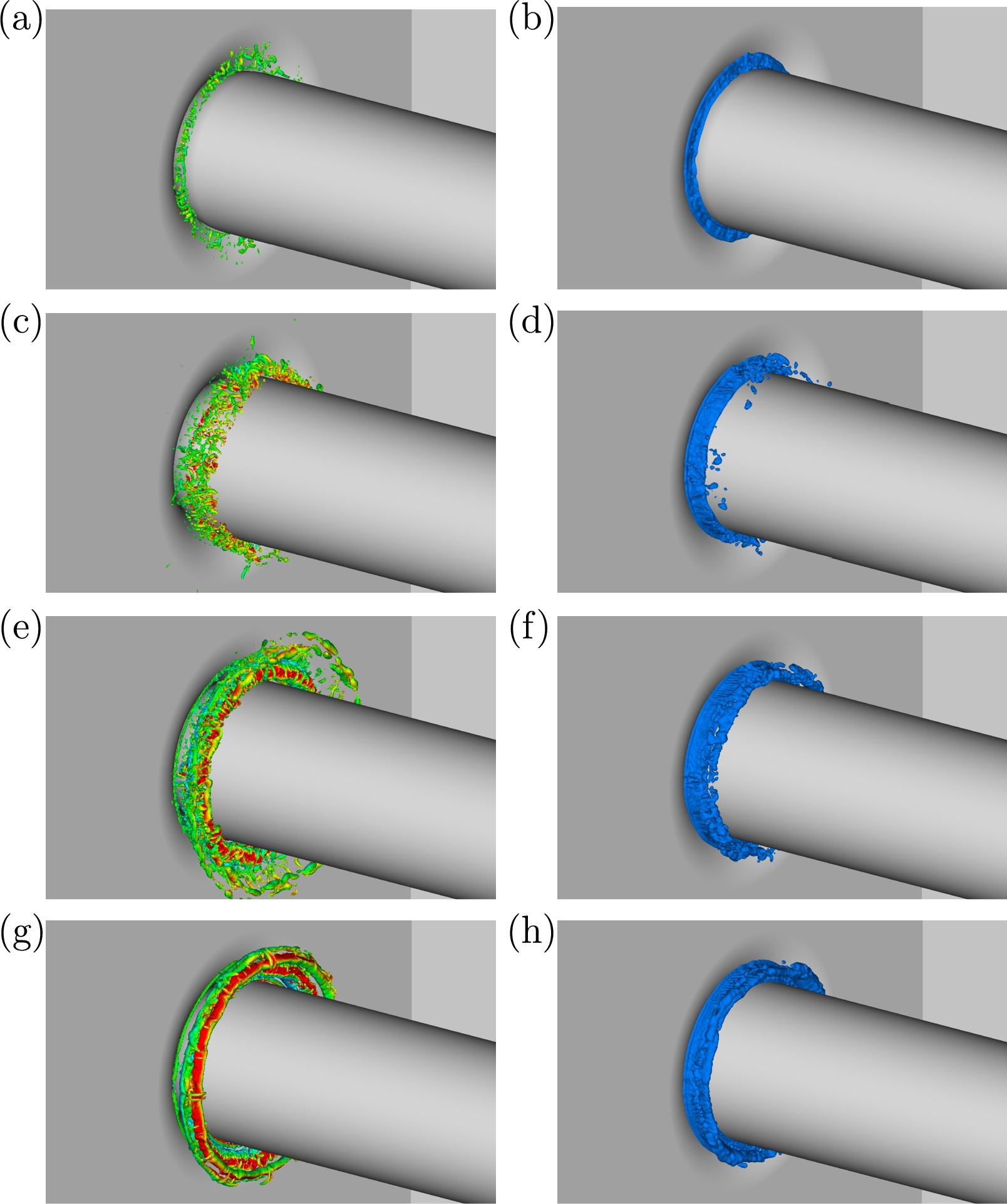
The new method is based on cut-elements. It provides sub-cell resolution of the geometry and handles flows through narrow closing or opening gaps in a straightforward manner. We validate our method with canonical flows around oscillating cylinders. We demonstrate that the method allows for an accurate prediction of flows around moving obstacles in weakly compressible liquid flows with cavitation effects. In particular, we show that the cavitating flow through a closing fuel injector control valve, which is an example for a complex application with interaction of stationary and moving parts, can be predicted by the method.

 

Computation of geometrical cut-cell properties based on (a) conventional level-set field Φ and (b) based on exact intersection with a provided surface triangulation.

 

Algorithm for computation of geometry parameters based on cut-elements. Construction of set of element corner vertices (top) and computation of wetted cell face area and fluid volume (bottom).

 

Cut-cell with multiple solid bodies. Effective face aperture is computed from individual contributions from each of the two solid bodies.

 

In-line oscillating cylinder in a fluid at rest (Re = 100 and KC = 5). Pressure (left) and vorticity contours (right) at four different phase-angles (top to bottom): 0°, 96°, 192°, 288°.

 

Time evolution of the in-line force acting on an oscillating cylinder in a fluid at rest for Reynolds number Re = 100 and Keulegan–Carpenter number KC = 5. Symbols denote reference experiment of Dütsch et al. (1998). Current simulation results: total drag — , viscous drag - - - , pressure drag — —. 

 

Geometry, mesh, and surface triangulation for the closing valve simulation.

 

Visualization of instantaneous iso-contours of the Q-criterion colored by the axial velocity (left column) and of the vapor fraction α = 0.05 (right column). Snapshots are taken at the same position of the valve needle Δx = 4.9 mm for a stationary needle and closing speeds of 1m/s, 2 m/s and 3 m/s (from top to bottom row).

Publications