J. Casacuberta, S. Hickel, S. Westerbeek, M. Kotsonis (2022)
Journal of Fluid Mechanics 943: A46. doi: 10.1017/jfm.2022.456
The interaction between forward-facing steps of several heights and a pre-existing critical stationary crossflow instability of a swept-wing boundary layer is analysed.
Direct numerical simulations (DNS) are performed of the incompressible three-dimensional laminar base flow and the stationary distorted flow that arise from the interaction between an imposed primary stationary crossflow perturbation and the steps. These DNS are complemented with solutions of the linear and the nonlinear parabolised stability equations, used towards identifying the influence of linearity and non-parallelism near the step. A fully stationary solution of the Navier–Stokes equations is enforced numerically, in order to isolate the mechanisms pertaining to the interaction of the stationary disturbance with the step.
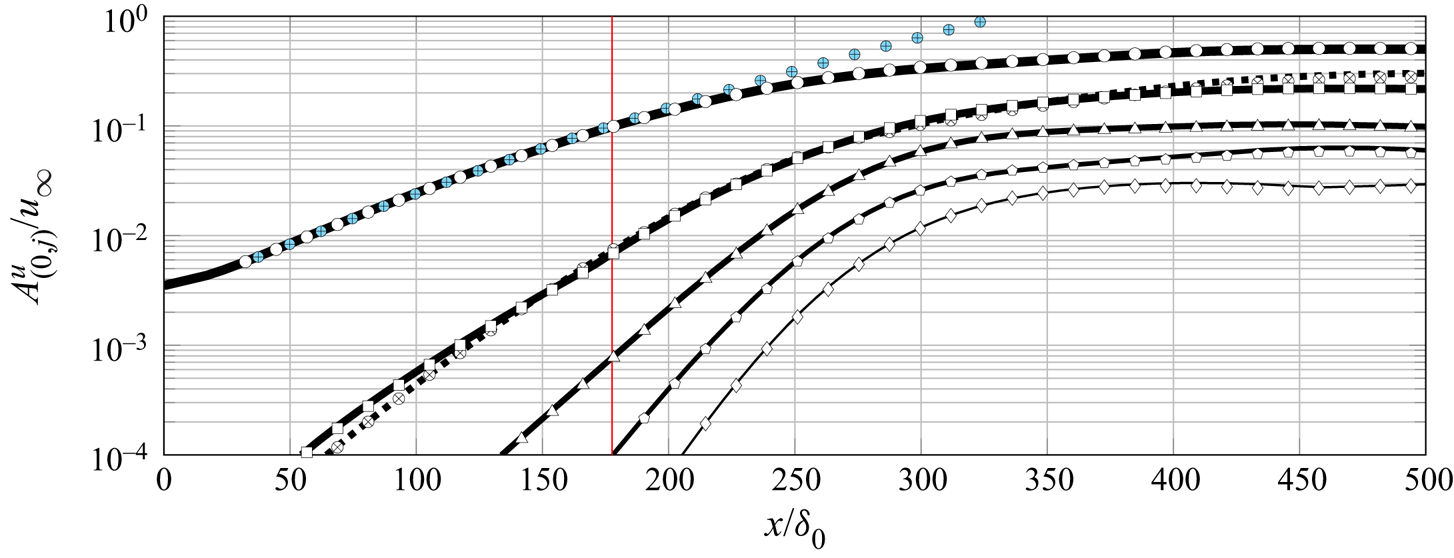
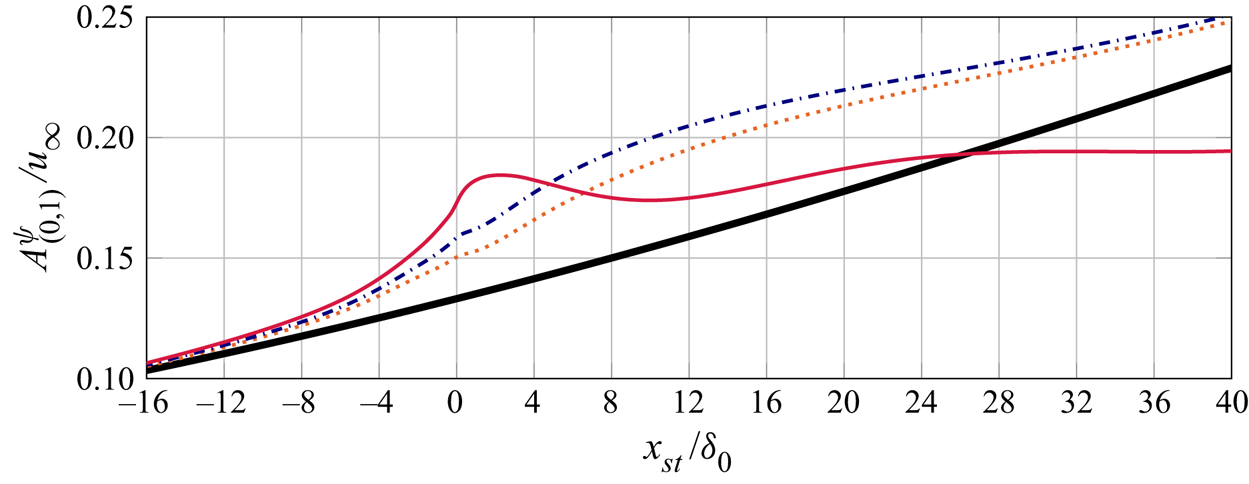
Results provide insight into the salient modifications of the base laminar boundary layer due to the step, and the response of the incoming crossflow instability to these changes. The fundamental spanwise Fourier mode of the disturbance field gradually lifts up as it approaches the step and passes over it. The flow environment around the step is characterised by a sudden spanwise modulation of the base-flow streamlines. Additional stationary perturbation structures are induced at the step, which manifest in the form of spanwise-aligned velocity streaks near the wall. Shortly downstream of the step, the fundamental component of the crossflow perturbation maintains a rather constant amplification for the smallest steps studied. For the largest step, however, the fundamental crossflow perturbation is stabilised significantly shortly downstream of the largest step. This surprising result is ascribed to a modulation of the kinetic energy transfer between the base flow and the fundamental perturbation field, which is brought forward as a new step interaction mechanism. Possible non-modal growth effects at the step are discussed. Furthermore, the results from DNS indicate significant amplification of the high-order harmonic crossflow components downstream of the step.