S. Hickel, N.A. Adams (2008)
International Journal of Heat and Fluid Flow 29: 626-639. doi: 10.1016/j.ijheatfluidflow.2008.03.008
Well resolved large-eddy simulations (LES) of a fully turbulent flat-plate boundary-layer flow subjected to a constant adverse pressure gradient are conducted. Flow parameters are adapted to an available experiment. The Reynolds number based on the local free-stream velocity and momentum thickness is 670 at the inflow and 5100 at the separation point. Clauser’s pressure-gradient parameter increases monotonically from 0 up to approximately 100 since a constant pressure gradient is prescribed. The adverse pressure gradient leads to a highly unsteady and massive separation of the boundary layer. The numerical predictions agree well with theory and experimental data.
Further development of LES faces as major obstacles the strong coupling between subgrid-scale (SGS) modeling and the truncation error of the numerical discretization. One can exploit this link by developing discretization methods where the truncation error itself functions as an implicit SGS model. The adaptive local deconvolution method (ALDM) is an approach to LES of turbulent flows that represents a full coupling of SGS model and discretization scheme. This paper provides evidence for the validity of this new SGS model.
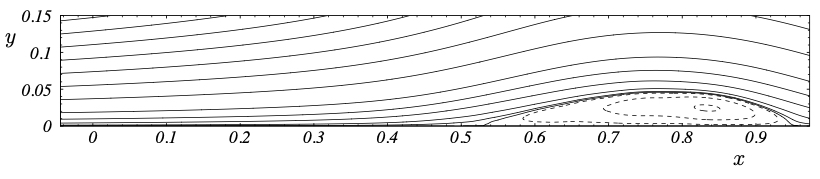

Instantaneous snapshot of vortical structures visualized by iso-surfaces of the Q criterion and flow separation visualized by the iso-surface of zero streamwise velocity.
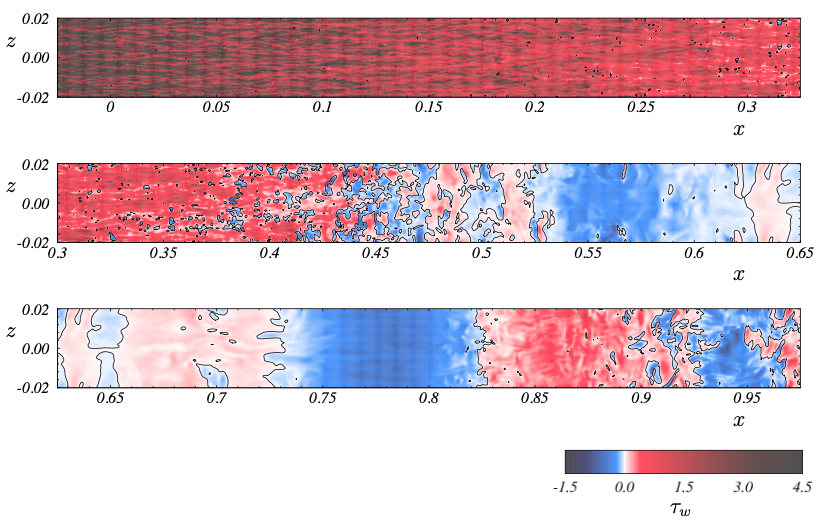
Instantaneous contours of the wall-shear stress.
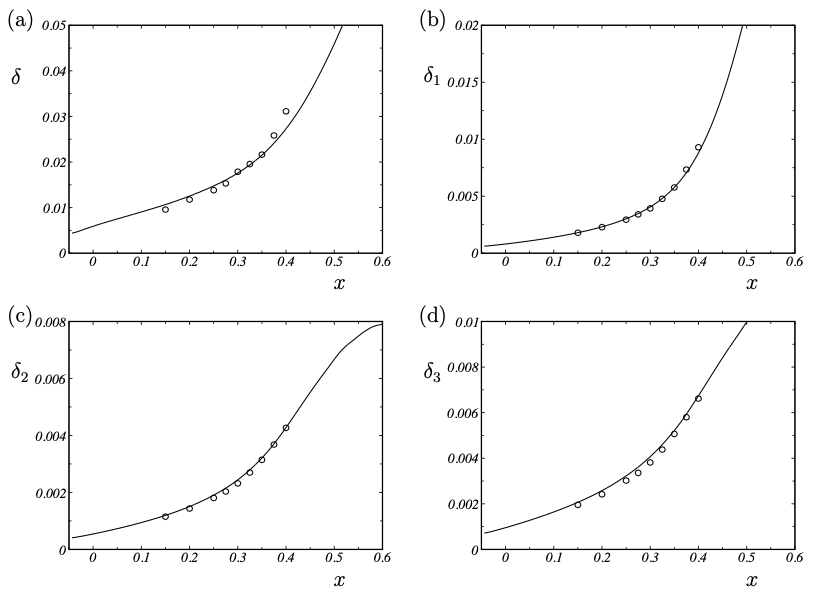
Integral measures for the boundary-layer thickness: (a) boundary-layer thickness, (b) displacement thickness, (c) momentum thickness, (d) energy thickness. − LES , ◦ measurement.
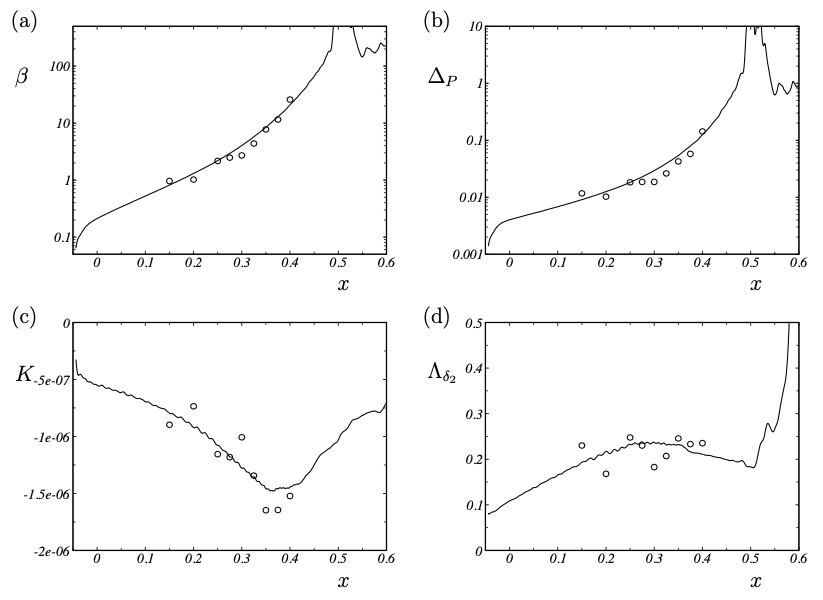
Pressure-gradient parameters (a) Clauser pressure-gradient parameter, (b) Patel pressure gradient, (c) dimensionless pressure-gradient parameter K, (d) dimensionless pressure-gradient parameter Λδ2 . − present LES , ◦ experiment.
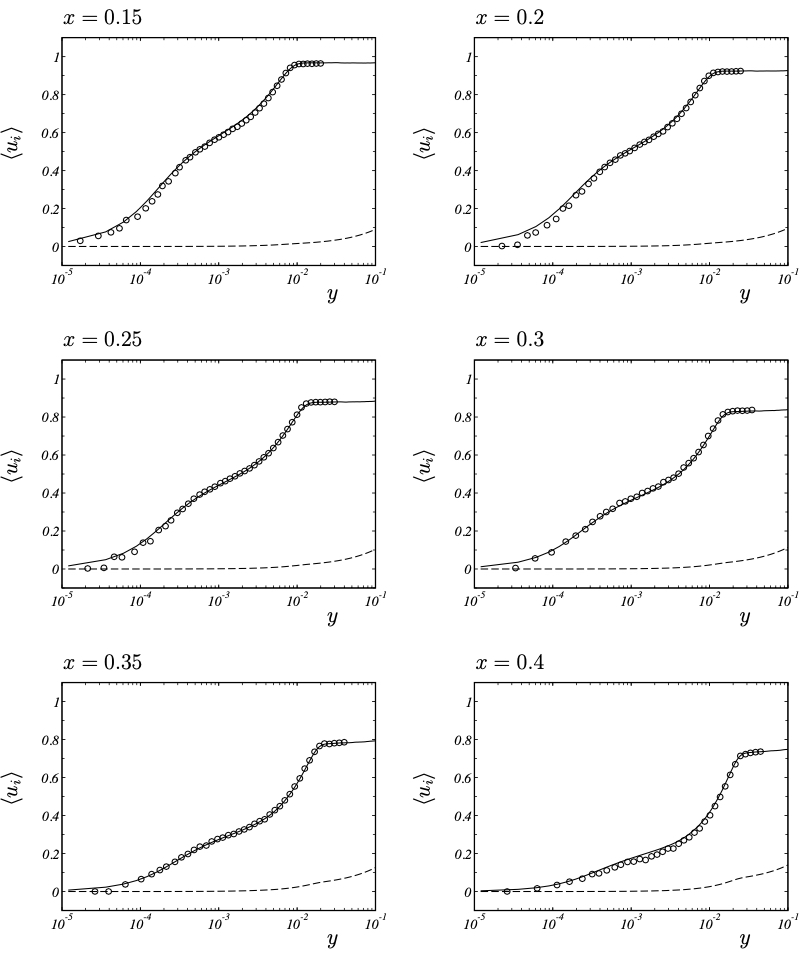
Mean velocity profiles (raw data) − ⟨u⟩ and −−−− ⟨v⟩ for LES, ◦ ⟨u⟩ for LDA measurements.
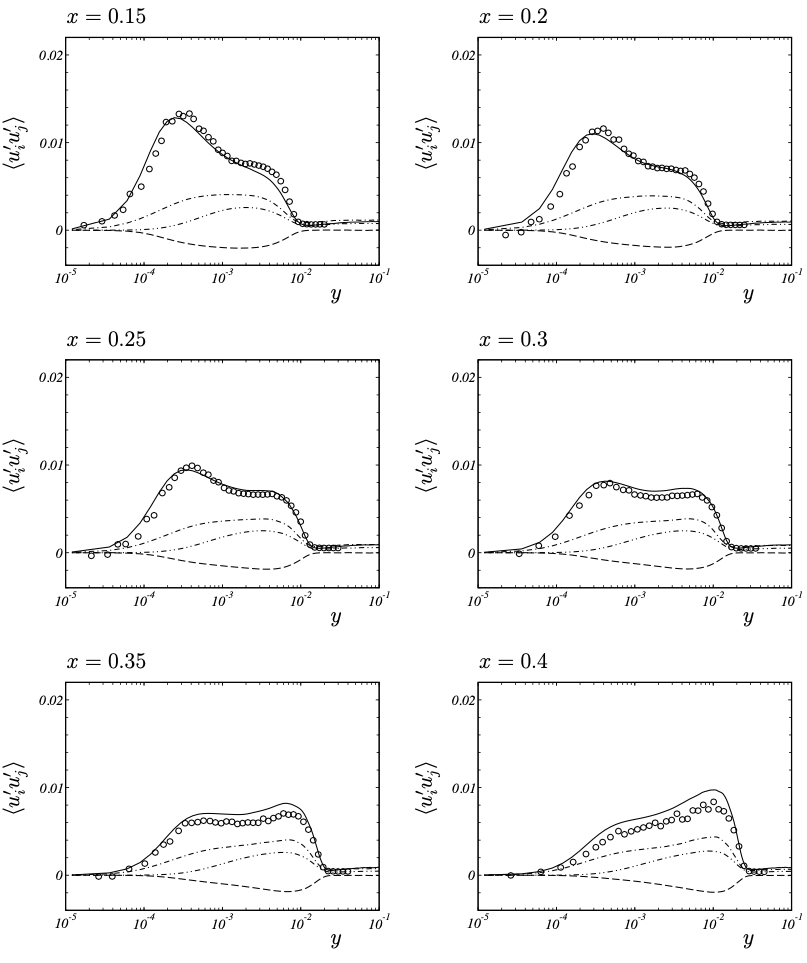
Reynolds stress tensor (raw data) − ⟨u′u′⟩ , −··−··− ⟨v′v′⟩ , ·−·−·− ⟨w′w′⟩ , and −−−− ⟨u′v′⟩ for LES, ◦ ⟨u′u′⟩ for LDA measurements.
