E. Lauer, X.Y. Hu, S. Hickel, N.A. Adams (2012)
Computers and Fluids 69: 1-19. doi: 10.1016/j.compfluid.2012.07.020
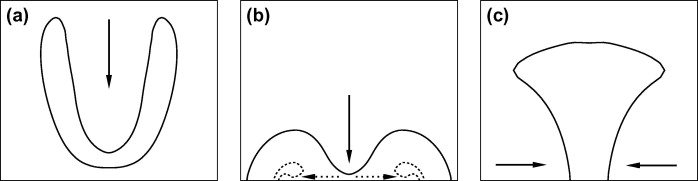
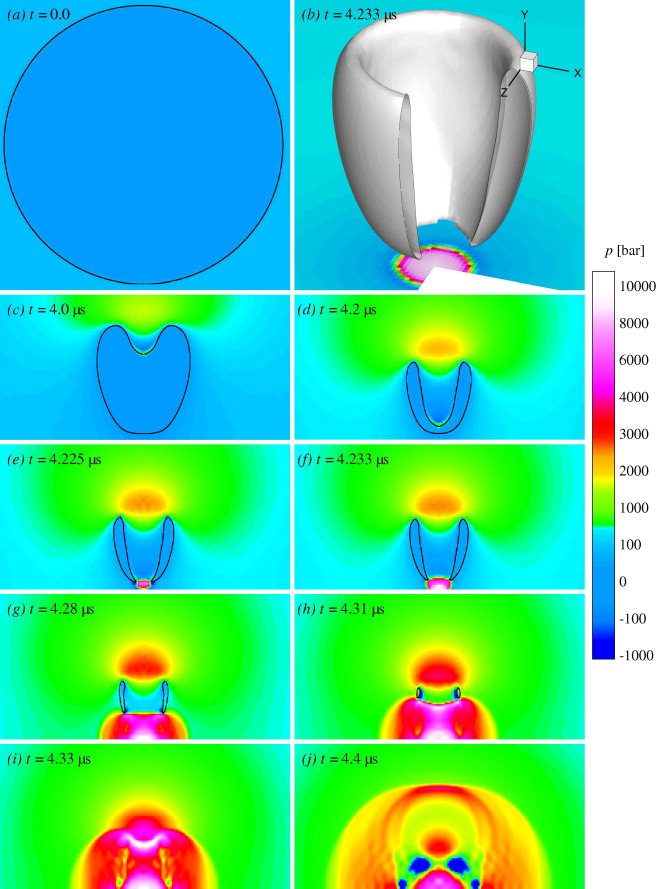
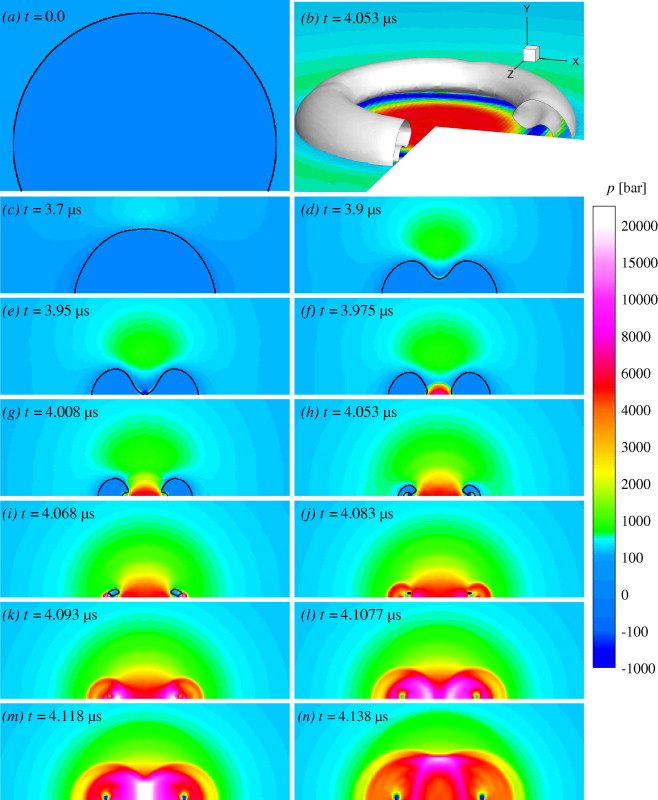
In this paper, we investigate the high-speed dynamics of symmetric and asymmetric cavitation bubble-collapse. For this purpose, a sharp-interface numerical model is employed, that includes a numerically efficient evaporation/condensation model.
The underlying assumption is that phase change occurs in thermal non-equilibrium and that the associated timescale is much larger than that of the wave-dynamics described by the interfacial Riemann problem. The sharp-interface model allows for an accurate tracking of the interface evolution throughout collapse and rebound. With a first set of simulations, we investigate the influence of the non-equilibrium on the relaxation behaviour of an oscillating vapour bubble. We observe that a good prediction of the phase-change rate is essential. Of high practical interest is the collapse of cavitation bubbles near walls under high ambient-pressure conditions. We investigate the differences in collapse evolution for detached and attached bubbles. It is shown that the maximum wall pressure strongly depends on the symmetry of the collapse mechanisms, and regions with a high probability of bubble rebound are identified. Asymmetric attached bubbles lead to significantly different topology changes during collapse than symmetric bubbles but exhibit roughly the same range of maximum pressures.