Computational Fluid Dynamics as good as it gets.

On the application of WKB theory for the simulation of the weakly nonlinear dynamics of gravity waves

J. Muraschko, M.D. Fruman, U. Achatz, S. Hickel, Y. Toledo (2015)
Quarterly Journal of the Royal Meteorological Society 141: 676-697. doi: 10.1002/qj.2381

The dynamics of internal gravity waves is modelled using Wentzel–Kramer–Brillouin (WKB) theory in position–wave number phase space. A transport equation for the phase-space wave-action density is derived for describing one-dimensional wave fields in a background with height-dependent stratification and height- and time-dependent horizontal-mean horizontal wind, where the mean wind is coupled to the waves through the divergence of the mean vertical flux of horizontal momentum associated with the waves.

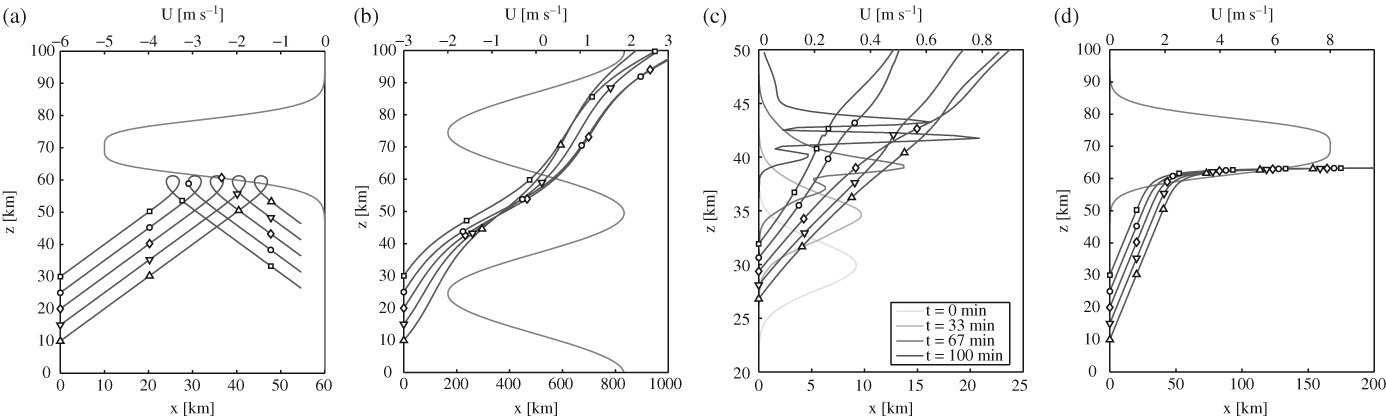
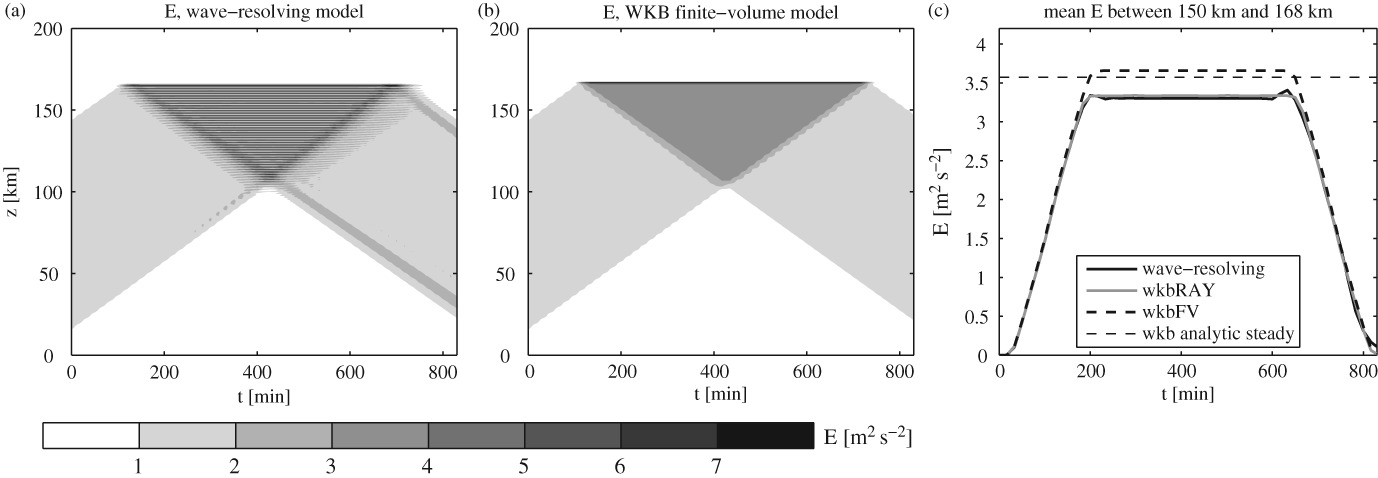
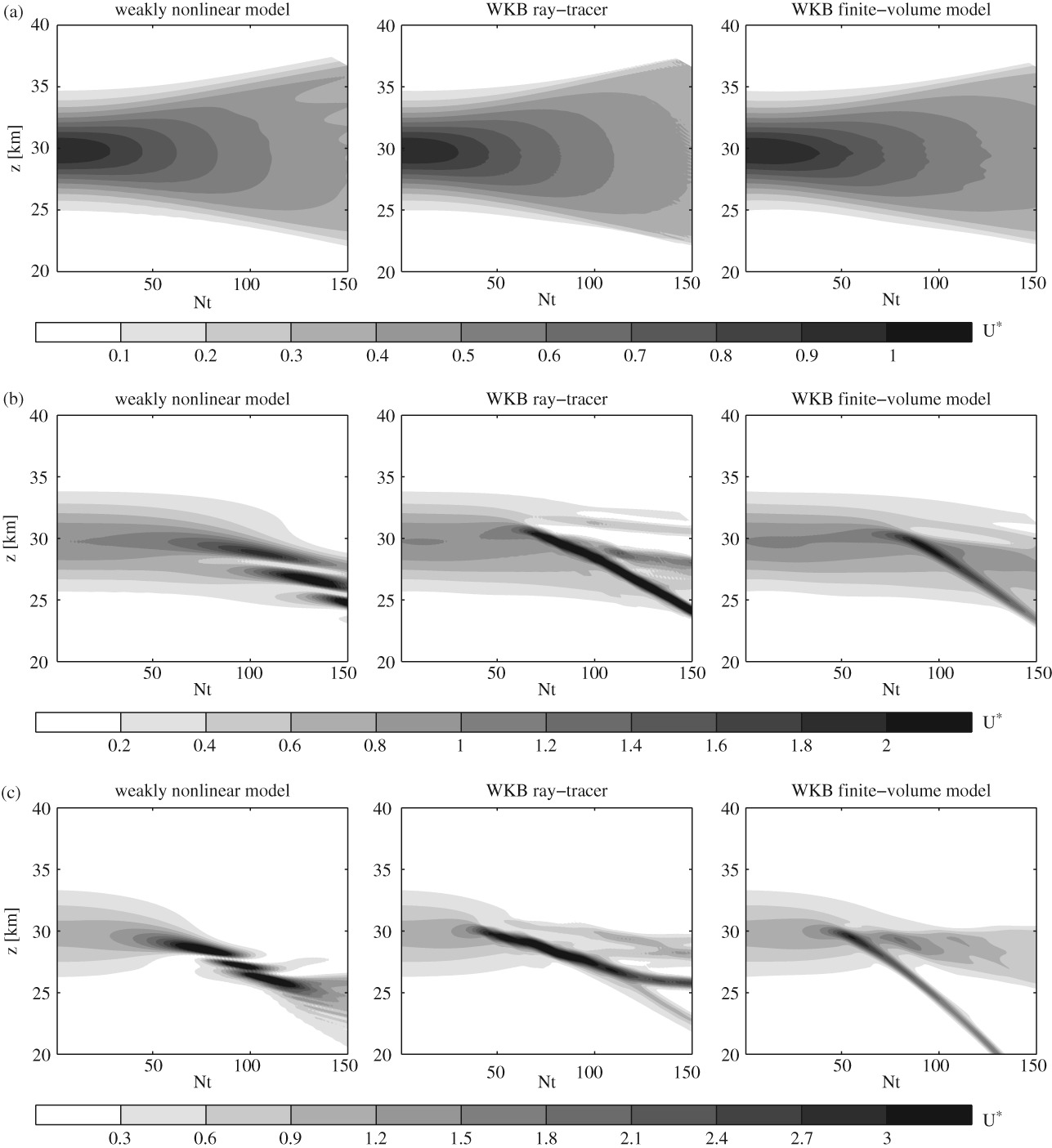
The phase-space approach bypasses the caustics problem that occurs in WKB ray-tracing models when the wave number becomes a multivalued function of position, such as in the case of a wave packet encountering a reflecting jet or in the presence of a time-dependent background flow. Two numerical models were developed to solve the coupled equations for the wave-action density and horizontal mean wind: an Eulerian model using a finite-volume method and a Lagrangian ‘phase-space ray tracer’ that transports wave-action density along phase-space paths determined by the classical WKB ray equations for position and wave number. The models are used to simulate the upward propagation of a Gaussian wave packet through a variable stratification, a wind jet and the mean flow induced by the waves. Results from the WKB models are in good agreement with simulations using a weakly nonlinear wave-resolving model, as well as with a fully nonlinear large-eddy-simulation model. The work is a step toward more realistic parametrizations of atmospheric gravity waves in weather and climate models.

 

Examples of the caustics problem in physical space: (a) rays (dark grey lines) associated with waves encountering a reflecting jet (light grey line); (b) waves propagating through a slowly varying alternating wind; (c) modulationally unstable waves propagating through their own induced mean flow; and (d) waves encountering a critical level due to a positive jet. Markers are placed along rays at intervals of (a, d) 100 min, (b) 500 min and (c) 33 min.

 

Horizontally averaged wave energy density of a very long wave packet reflected by a wind jet from (a) the wave-resolving linear model and (b) the WKB models (in linear mode). (c) Mean energy in the layer between 150 and 168 km as a function of time. Once the downward (outgoing) waves balance the upward (incoming) waves, the wave energy reaches a plateau at the value corresponding to a case of a steady wave train reflected by a jet. The energy in the layer predicted by the analytic solution to the steady-state WKB problem is indicated by the dashed horizontal line.

 

Normalized wave-induced mean flow from the modulational instability experiment simulated with the weakly nonlinear wave-resolving model and both WKB models: (a) stable case (m0 = −1.4k, a0 = 0.12), (b) metastable case (m0 = −0.7k, a0 = 0.21) and (c) unstable case (m0 = −0.4k, a0 = 0.42). Plots are in the reference frame moving with the initial group speed at the centre of the wave packet.

Publications