Computational Fluid Dynamics as good as it gets.

Rapid multi-component phase-split calculations using volume functions and reduction methods

M. Fathi, S. Hickel (2021)
AIChE Journal 67: e17174. doi: 10.1002/aic.17174

We present a new family of fast and robust methods for the calculation of the vapor–liquid equilibrium at isobaric-isothermal (PT-flash), isochoric-isothermal (VT-flash), isenthalpic-isobaric (HP-flash), and isoenergetic-isochoric (UV-flash) conditions. The framework is provided by formulating phase-equilibrium conditions for multi-component mixtures in an effectively reduced space based on the molar specific value of the recently introduced volume function derived from the Helmholtz free energy.

The proposed algorithmic implementation can fully exploit the optimum quadratic convergence of a Newton method with the analytical Jacobian matrix. This article provides all required exact analytic expressions for the general cubic equation of state.

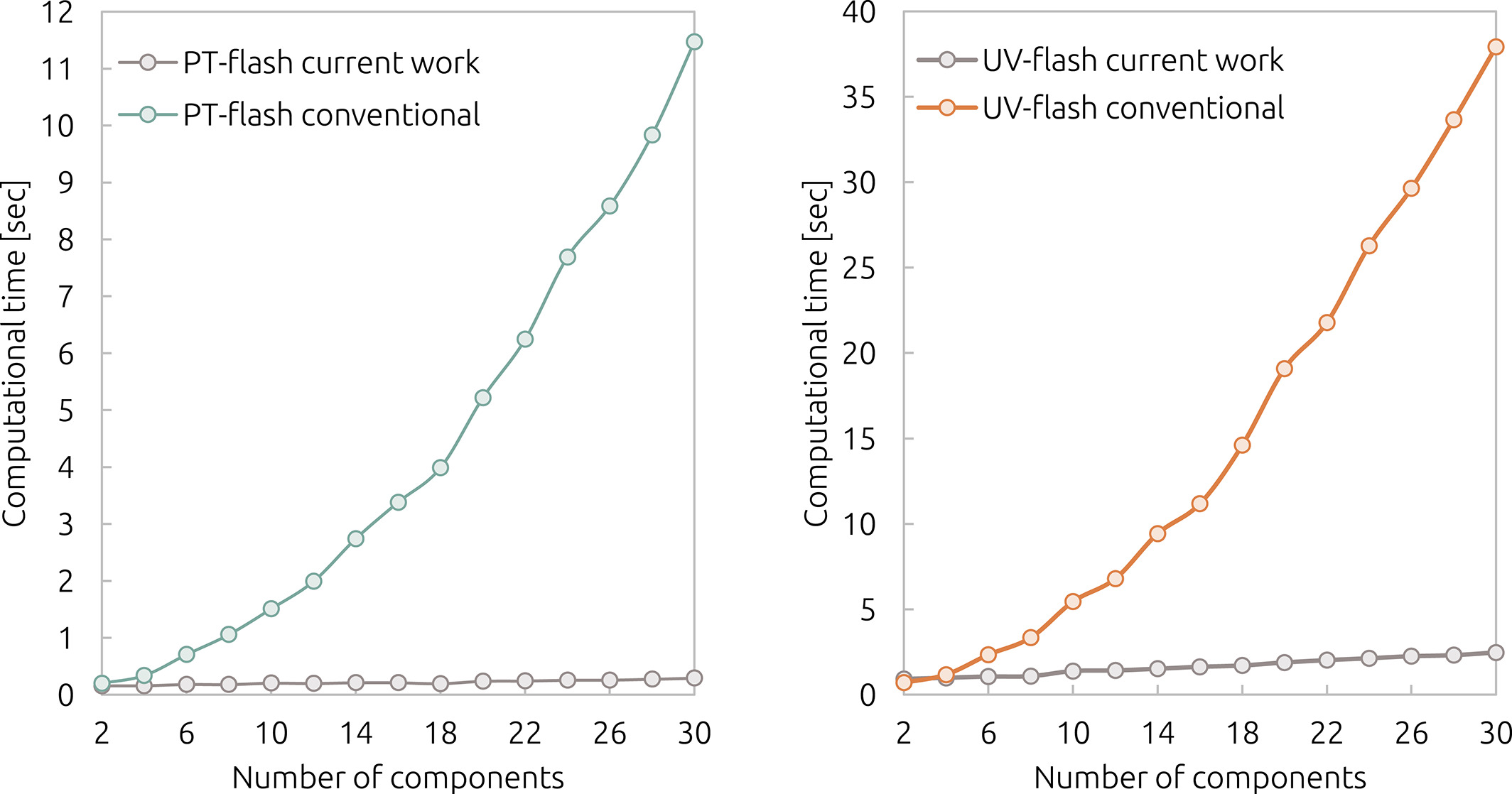
Computational results demonstrate the effectivity and efficiency of the new methods. Compared to conventional methods, the proposed reduced-space iteration leads to a considerable speed-up as well as to improved robustness and better convergence behavior near the spinodal and coexistence curves of multi-component mixtures, where the preconditioning by the reduction method is most effective.

Phase diagram of binary mixtures of n-heptane and ethane at various molar compositions computed by the proposed algorithm. The symbols denote experimental reference data for the dew-point and bubble-point lines. The black box encloses the pressure–temperature domain that was used for measuring the computational performance of the flash algorithms.
Computational time for PT-flashes and UV-flashes versus number of mixture components. Shown is the total CPU time for 100 × 100 flash calculations in the highlighted region of the above phase diagram. The computational time for the current PT-flash algorithm is always lower than the highly optimized reference method. The performance gain becomes increasingly significant as the number of components is increased, which shows the importance of reduction methods for the both iso-thermal and non-isothermal flashes. Surprisingly, we also measure a cost benefit for the two-component mixture, where the number of variables is not reduced by the new method. In this case, the reduction method acts as a preconditioner and reduces the number of required iterations for the PT-flash.

Publications