J. Casacuberta, K.J. Groot, Q. Ye, S. Hickel (2020)
Flow Turbulence and Combustion 104: 533-552. doi: 10.1007/s10494-019-00085-1
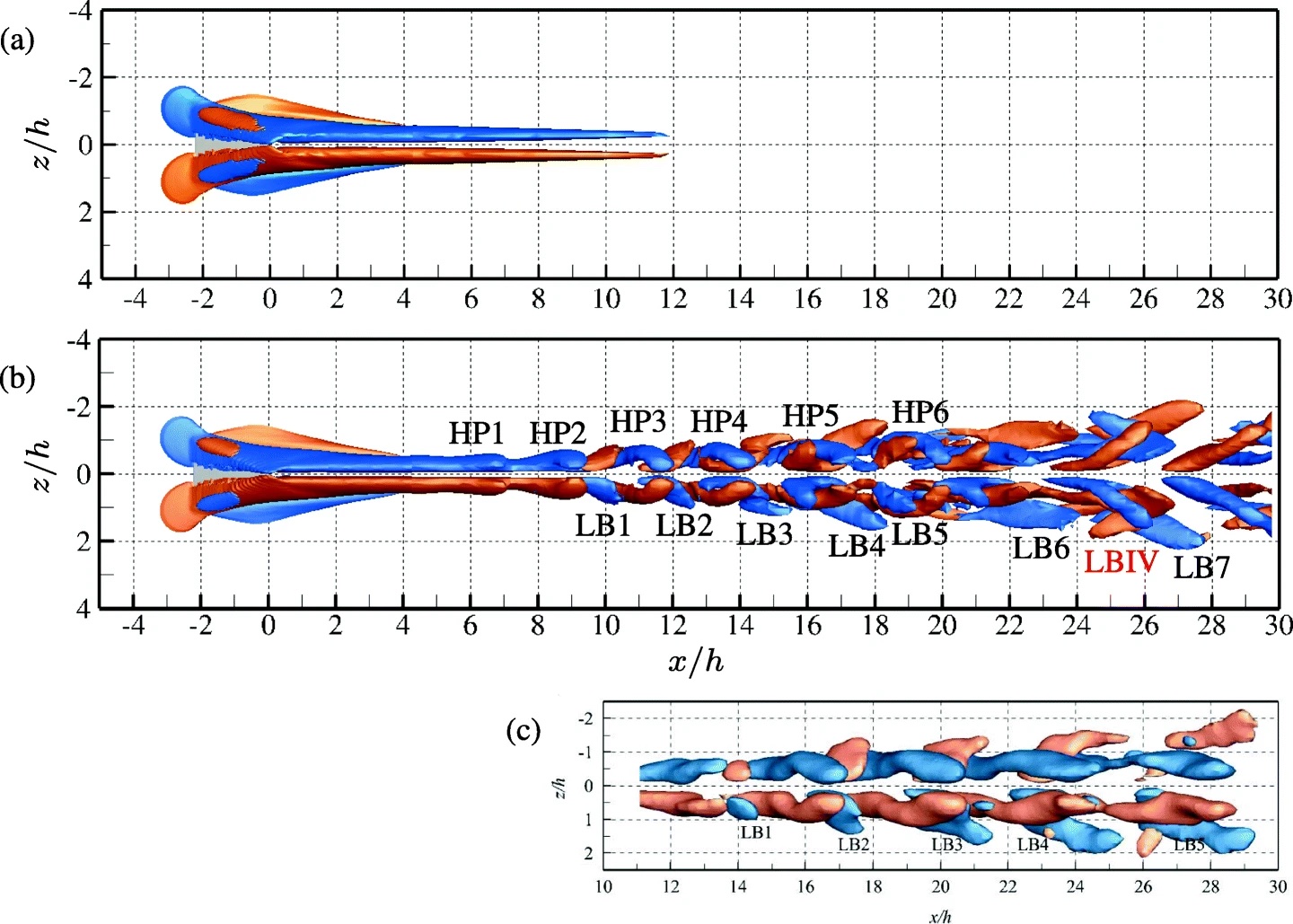
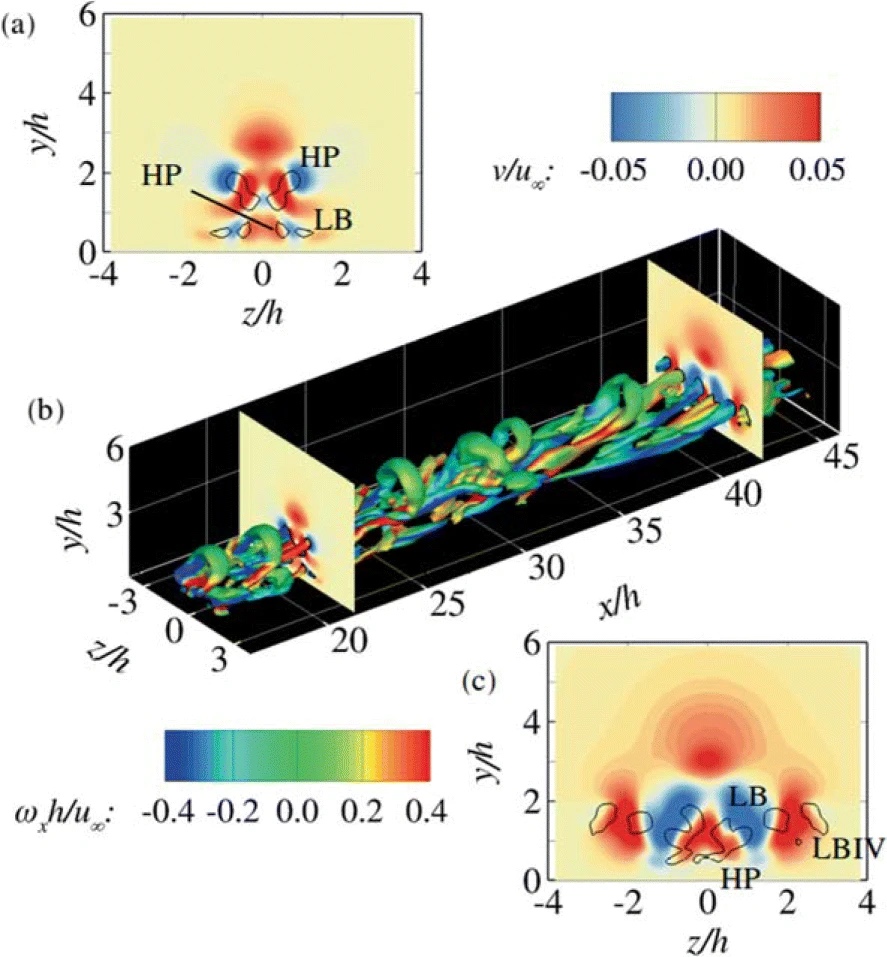
Micro-ramps are popular passive flow control devices which can delay flow separation by re-energising the lower portion of the boundary layer. We compute the laminar base flow, the instantaneous transitional flow, and the mean flow around a micro-ramp immersed in a quasi-incompressible boundary layer at supercritical roughness Reynolds number.
Results of our Direct Numerical Simulations (DNS) are compared with results of BiLocal stability analysis on the DNS base flow and independent tomographic Particle Image Velocimetry (tomo-PIV) experiments. We analyse relevant flow structures developing in the micro-ramp wake and assess their role in the micro-ramp functionality, i.e., in increasing the near-wall momentum. The main flow feature of the base flow is a pair of streamwise counter-rotating vortices induced by the micro-ramp, the so-called primary vortex pair. In the instantaneous transitional flow, the primary vortex pair breaks up into large-scale hairpin vortices, which arise due to linear varicose instability of the base flow, and unsteady secondary vortices develop. Instantaneous vortical structures obtained by DNS and experiments are in good agreement. Matching linear disturbance growth rates from DNS and linear stability analysis are obtained until eight micro-ramp heights downstream of the micro-ramp. For the setup considered in this article, we show that the working principle of the micro-ramp is different from that of classical vortex generators; we find that transitional perturbations are more efficient in increasing the near-wall momentum in the mean flow than the laminar primary vortices in the base flow.