Computational Fluid Dynamics as good as it gets.

Large-eddy simulation of cavitating nozzle flow and primary jet break-up

F. Örley, T. Trummler, S. Hickel, M.S. Mihatsch, S.J. Schmidt, N.A. Adams (2015)
Physics of Fluids 27: 086101. doi: 10.1063/1.4928701

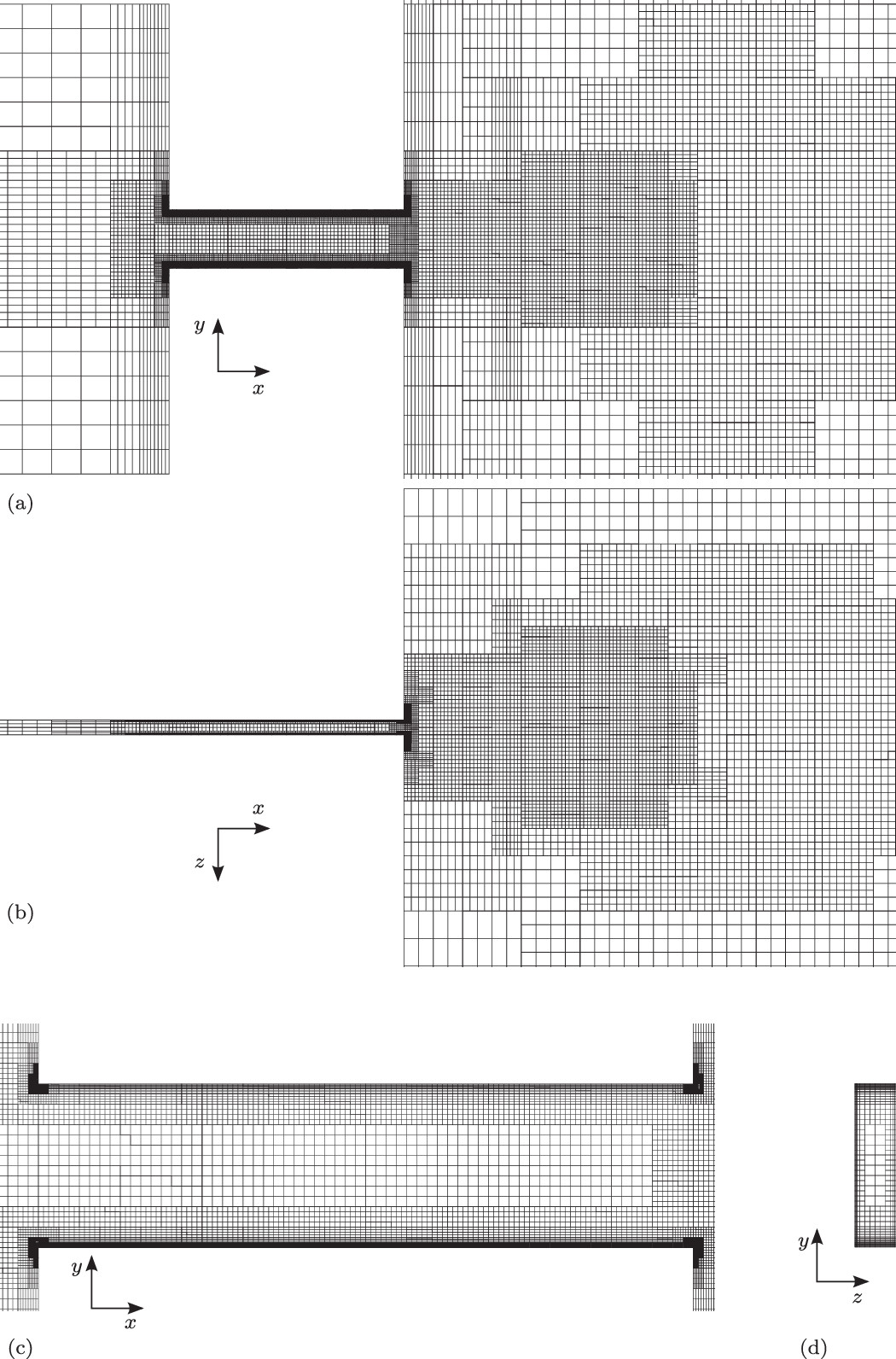
We employ a barotropic two-phase/two-fluid model to study the primary break-up of cavitating liquid jets emanating from a rectangular nozzle, which resembles a high aspect-ratio slot flow. All components (i.e., gas, liquid, and vapor) are represented by a homogeneous mixture approach. The cavitating fluid model is based on a thermodynamic-equilibrium assumption. Compressibility of all phases enables full resolution of collapse-induced pressure wave dynamics.

The thermodynamic model is embedded into an implicit large-eddy simulation (LES) environment. The considered configuration follows the general setup of a reference experiment and is a generic reproduction of a scaled-up fuel injector or control valve as found in an automotive engine. Due to the experimental conditions, it operates, however, at significantly lower pressures. LES results are compared to the experimental reference for validation. Three different operating points are studied, which differ in terms of the development of cavitation regions and the jet break-up characteristics. Observed differences between experimental and numerical data in some of the investigated cases can be caused by uncertainties in meeting nominal parameters by the experiment. The investigation reveals that three main mechanisms promote primary jet break-up: collapse-induced turbulent fluctuations near the outlet, entrainment of free gas into the nozzle, and collapse events inside the jet near the liquid-gas interface.

 

Computational grid of the full computational domain: (a) x-y view in the z symmetry plane; (b) x-z view in the y symmetry plane; (c) x-y view in the z symmetry plane of the nozzle region; (d) y-z view in the nozzle cross section. Only every fourth grid line is shown.

 

Snapshot of iso-surfaces of λ2 = − 1 × 108 1/s2 colored by streamwise velocity u (left column) together with iso-surfaces of vapor volume fraction α = 0.1 and wall pressure (right column) for σ = 1.27, σ = 0.78, and σ = 0.65 (from top to bottom).

 

Experimental transmitted light images (left column, reprinted with permission from A. Sou, S. Hosokawa, and A. Tomiyama, “Effects of cavitation in a nozzle on liquid jet atomization,” Int. J. Heat Mass Transfer 50, 3575 (2007). Copyright 2007 Elsevier) and LES snapshots of x-y view (middle column) and x-z view (right column) showing iso-surfaces of gas volume fraction βG = 0.99 in the range 16 mm < x < 32 mm for σ = 1.27, σ = 0.78, and σ = 0.65 (from top to bottom).

Publications