M.D. Fruman, S. Remmler, U. Achatz, S. Hickel (2014)
Journal of Geophysical Research 119: 11613-11640. doi: 10.1002/2014JD022046
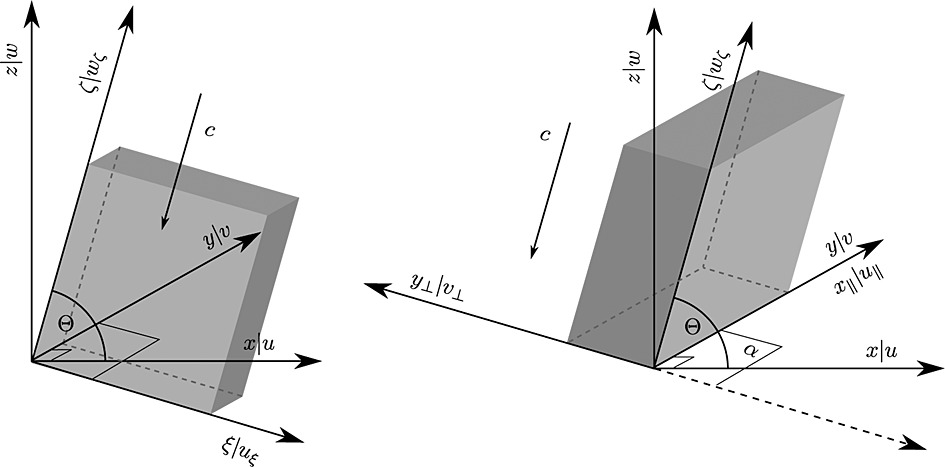
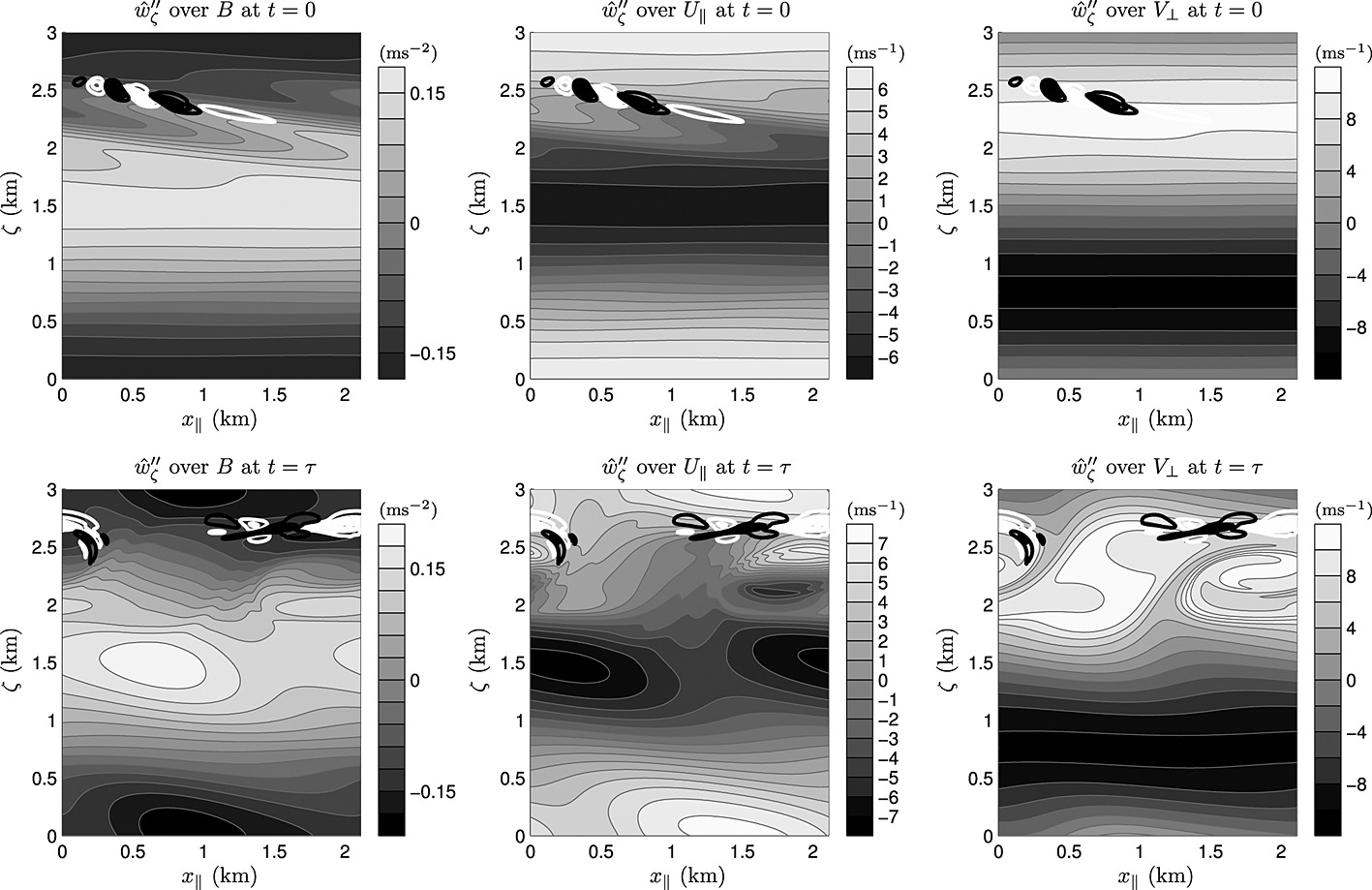
A systematic approach to the direct numerical simulation (DNS) of breaking upper mesospheric inertia-gravity waves of amplitude close to or above the threshold for static instability is presented. Normal mode or singular vector analysis applied in a frame of reference moving with the phase velocity of the wave (in which the wave is a steady solution) is used to determine the most likely scale and structure of the primary instability
and to initialize nonlinear “2.5-D” simulations (with three-dimensional velocity and vorticity fields but depending only on two spatial coordinates). Singular vector analysis is then applied to the time-dependent 2.5-D solution to predict the transition of the breaking event to three-dimensional turbulence and to initialize three-dimensional DNS. The careful choice of the computational domain and the relatively low Reynolds numbers, on the order of 25,000, relevant to breaking waves in the upper mesosphere, makes the three-dimensional DNS tractable with present-day computing clusters. Three test cases are presented: a statically unstable low-frequency inertia-gravity wave, a statically and dynamically stable inertia-gravity wave, and a statically unstable high-frequency gravity wave. The three-dimensional DNS are compared to ensembles of 2.5-D simulations. In general, the decay of the wave and generation of turbulence is faster in three dimensions, but the results are otherwise qualitatively and quantitatively similar, suggesting that results of 2.5-D simulations are meaningful if the domain and initial condition are chosen properly.